You have probably already heard the horror stories of code interviews where they ask you to reverse a binary tree on a whiteboard. (if not check this blog post that I profoundly disagree with)

Well, a few days ago I was in that exact situation. And I had no idea what the interviewer was talking about. So what are these binary trees and why is it so critical that you know how to inverse them? Let’s find out.

What is a binary tree

A binary tree is a very simple data structure that as the name suggests looks like an upside down tree.

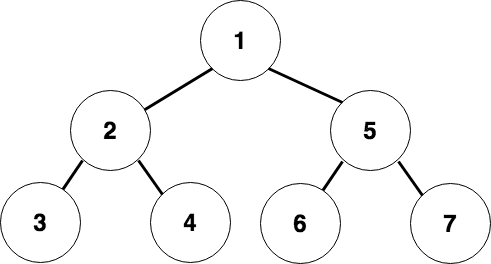
This structure is mainly used for searching. For example, if we needed to find 4 in this structure quickly, we would need only to make 2 binary decisions. If we scale this up to 1000 nodes, we would only need about 10 choices. There are other options still, like self-balancing binary trees but let’s keep it simple at the moment, and just focus on balanced binary trees.

Let’s invert them

Ok so now that we know what it is let’s start with inverting a binary tree. What do we mean by that? It’s actually very straightforward. We turn this:

      4
     /  \
    2    7
   / \  / \
  1  3 6   9

into

     4
    /  \
   7    2
  / \  / \
 9  6 3   1

We flip the entire structure horizontally. So 7 and 2 are flipped, and the 2 children are also flipped. All the way down.

Down to code

As we are good OOP developers, we are first going to start with our tree. A binary tree is nothing more than a collection of points, called nodes, with 2 children: a left and a right one. So first we are going to create a Node object.

<?php

class Node
{
    private $value;
    private $left;
    private $right;

    public function __construct(string $value, ?Node $left, ?Node $right)
    {
        $this->left = $left;
        $this->right = $right;
        $this->value = $value;
    }

    public function getValue(): string
    {
        return $this->value;
    }

    public function getLeft(): ?Node
    {
        return $this->left;
    }

    public function getRight(): ?Node
    {
        return $this->right;
    }
}

(I’ve added value to the object as well, just to give it a practical use)

Now that we have the Node object it’s time to create a tree.

<?php

$level3al = new Node('deepAL', null, null);
$level3ar = new Node('deepAR', null, null);

$level3bl = new Node('deepBL', null, null);
$level3br = new Node('deepBR', null, null);

$level2a = new Node('midA', $level3al, $level3ar);
$level2b = new Node('midB', $level3bl, $level3br);

$level1 = new Node('top', $level2a, $level2b);

At this point we have a data structure that looks like this:

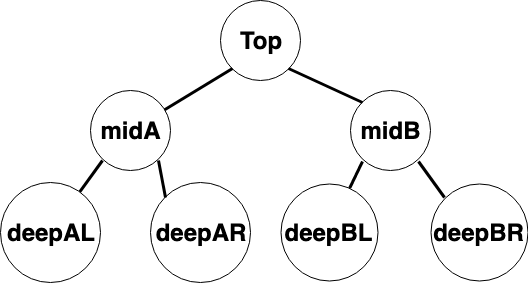
This is all set up, time to move on to the swapping. If we break the problem down to its core, we just want to swap the children of a node. Like this:

<?php

public function invert(Node $tree): Node
{
    $right = $tree->getLeft();
    $left = $tree->getRight();

    return new Node($tree->getValue(), $left, $right);
}

We take the Node and create (and return) a new Node with the children swapped. We now have:

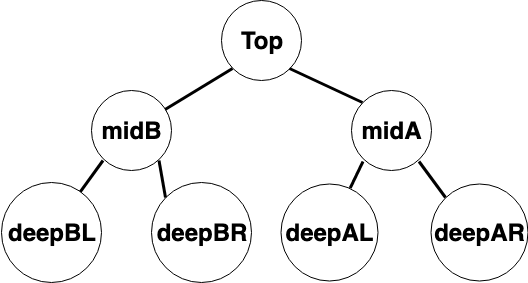
At first, glance that looks like we completed the task, but if you look a tiny bit deeper, you might see that we only inverted one level. The lower levels are in the same place (but on the other side of the branch).

To switch those we actually just have to repeat this process till we run out of levels. Now that sounds like a recursive function.

<?php

public function invert(?Node $tree): ?Node
{
    if ($tree === null) {
        return null;
    }

    $right = $this->invert($tree->getLeft());
    $left = $this->invert($tree->getRight());

    return new Node($tree->getValue(), $left, $right);
}

Let’s run through it:

The first thing to note is that our function signature changed. We now also accept null values. Why? Well once we hit bottom, there aren’t any children left. getRight() will return null. This null will indicate that we are at the end of our loop.

next up is that if check:

        if ($tree === null) {
            return null;
        }

This is that check for when we run into a null value as described above.

Now the meat of the algorithm:

    $right = $this->invert($tree->getLeft());
    $left = $this->invert($tree->getRight());

    return new Node($tree->getValue(), $left, $right);

This is the recursive method. Every time we pass this, we go one level deeper. If we hit bottom, that if will take care of it and it stops. If not, we swap the values and bubble it back up to the level above.

That’s it. Inverting a binary tree is 10 lines of code. It’s actually pretty simple.

Cool, so when would I actually want to inverse a Binary tree?

I have no idea. I’m sure some brilliant people on Reddit or Twitter will have a trove of useful functionality, but I sure can’t think of one.

In my opinion, this is just one of those job interview questions that solely exist so the interviewer can feel smart. You could argue that this is a simple test to see if the candidate can think recursively, but I believe that an open conversation about the interests of the candidate + maybe a small take-home test would give way more insights.